关联矩阵(incidence matrix)
我们生成的这个矩阵的原型是一个引证关系矩阵。 矩阵中的三行代表3篇文献,四列代表4篇引文。 1/2/3/4是在A/B/C前面发表的文献,A/B/C是后来发表的文献。 其中文献A引用了3/4,文献B引用了1/2/4,文献C引用了1/2/4。
library(igraph)
library(Matrix)
set.seed(3)
m <- matrix(data = sample(0:1, 12, replace = TRUE),nrow = 3)
rownames(m) <- LETTERS[1:3]
colnames(m) <- 1:4
m
## 1 2 3 4
## A 0 0 1 1
## B 1 1 0 1
## C 1 1 0 1
这样的一个引证关系,可以用下面的图表示。
在bibliometrix::cocMatrix() 中将这种矩阵称为共现矩阵,Co-occurrence Matrix。
par(mar=c(1,1,1,1))
g1 <- graph_from_incidence_matrix(m,directed = TRUE,mode = "out")
## Warning: `graph_from_incidence_matrix()` was deprecated in igraph 1.6.0.
## ℹ Please use `graph_from_biadjacency_matrix()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.
plot(g1)
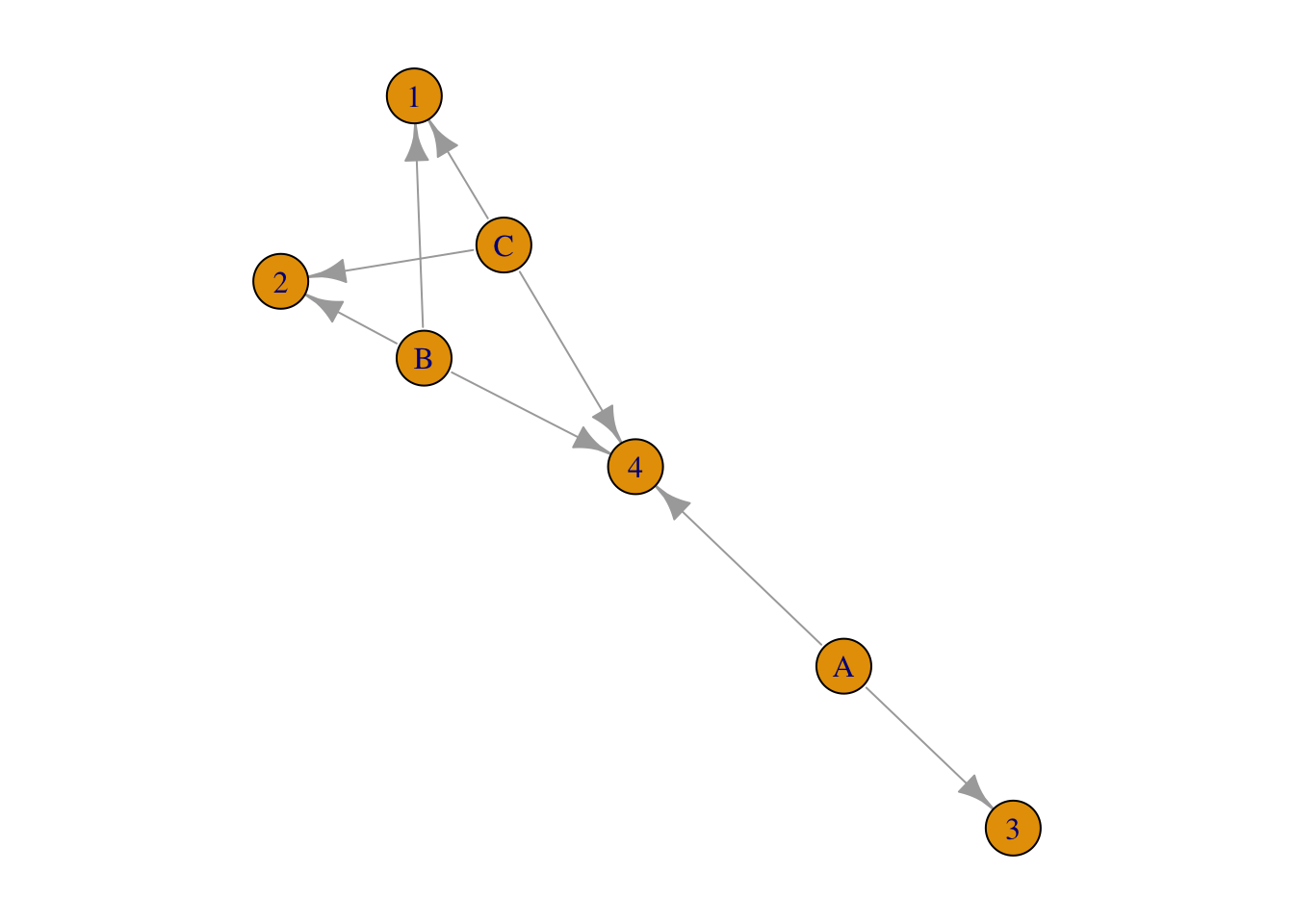
上面的矩阵通过矩阵叉乘可以得到不同的邻接矩阵,用于生成新的网络。
矩阵和向量的计算
矩阵的点乘就是矩阵各个对应元素相乘, 这个时候要求两个矩阵必须同样大小。
https://blog.csdn.net/u013066730/article/details/57462299
矩阵的叉乘(乘法)就是矩阵A的第一行乘以矩阵B的第一列,各个元素对应相乘然后求和作为第一元素的值。 矩阵只有当左边矩阵的列数等于右边矩阵的行数时才可以相乘, 乘积矩阵的行数等于左边矩阵的行数,乘积矩阵的列数等于右边矩阵的列数。
向量的点乘和叉乘是矩阵算法的基础。
https://blog.csdn.net/dcrmg/article/details/52416832
向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算, 就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影。
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
在 R 语言中,使用 %*% 计算矩阵的叉乘,而 crossprod() 和 tcrossprod() 函数对算法进行了优化。
此外,crossprod() 对计算过程也进行了变动,同一个矩阵的叉乘时不需要预先转置。
下面的三个个计算结果一样。
m %*% t(m)
## A B C
## A 2 1 1
## B 1 3 3
## C 1 3 3
crossprod(t(m),t(m))
## A B C
## A 2 1 1
## B 1 3 3
## C 1 3 3
tcrossprod(m,m)
## A B C
## A 2 1 1
## B 1 3 3
## C 1 3 3
下面的两个结果也一样。
t(m) %*% m
## 1 2 3 4
## 1 2 2 0 2
## 2 2 2 0 2
## 3 0 0 1 1
## 4 2 2 1 3
crossprod(m,m)
## 1 2 3 4
## 1 2 2 0 2
## 2 2 2 0 2
## 3 0 0 1 1
## 4 2 2 1 3
邻接矩阵(adjacency matrix)
m2 <- crossprod(m,m)
m2
## 1 2 3 4
## 1 2 2 0 2
## 2 2 2 0 2
## 3 0 0 1 1
## 4 2 2 1 3
共被引(co-citation)是指当两篇(或多篇)文献同时被后来一篇(或多篇)论文所引用的关系, 同时引用这两篇论文的文献数目则称为共被引强度。 文献的共被引关系会随着时间的变化而变化。 通过对文献共被引网络的研究可以探究科学的发展和演进动态。
根据共被引的定义,文献1和2同时被B和C引用,二者具有共被引关系,共被引强度是2。 同理,文献3和4之间的共被引强度是1, 文献1和3的共被引强度是0,文献2和3的共被引强度是0; 文献2和4的共被引强度是2,文献1和4的共被引强度是2。
g2 <- graph_from_adjacency_matrix(m2, mode = "undirected")
par(mar=c(1,1,1,1))
plot(g2,layout=layout_with_kk)
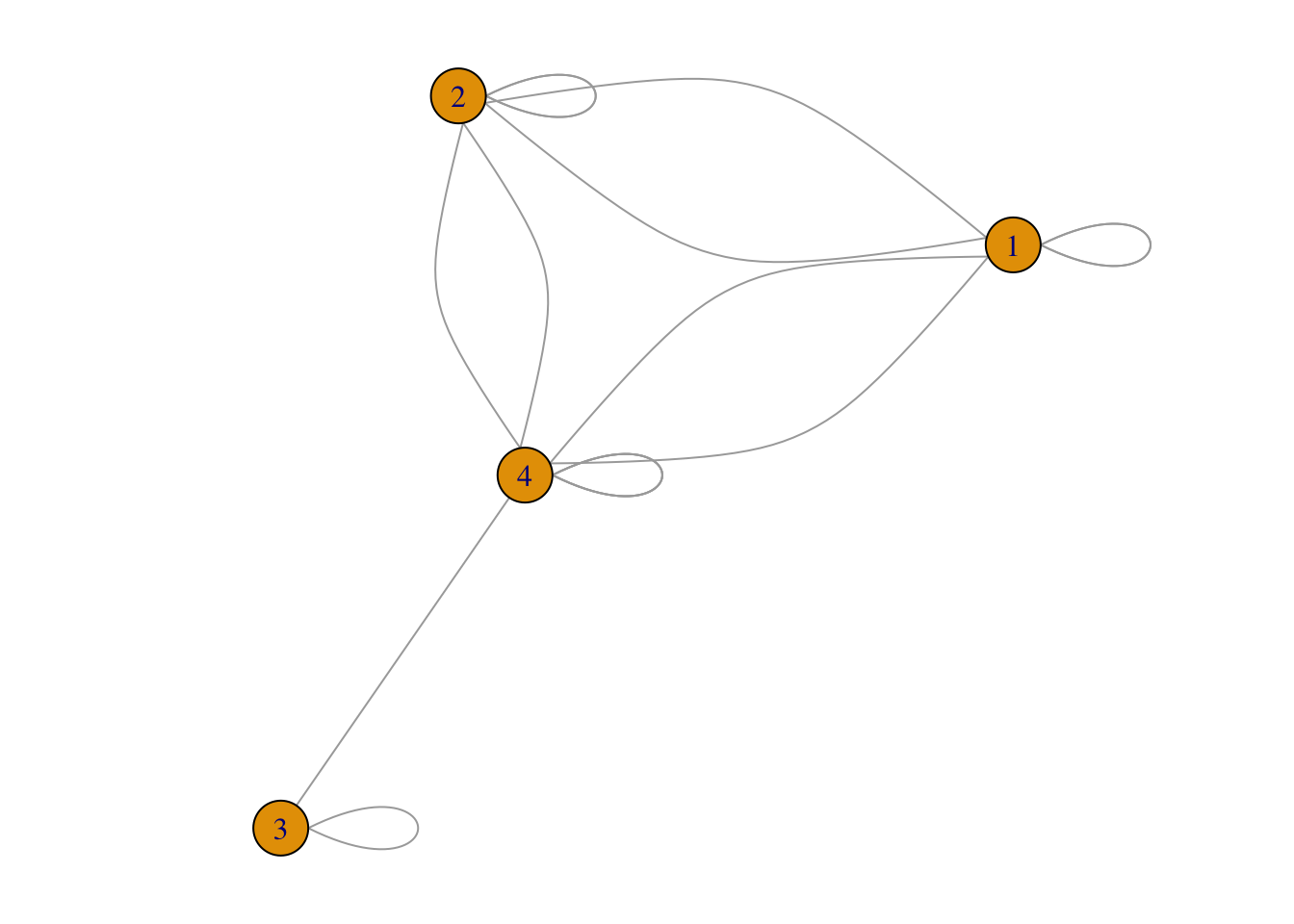
若文献A和文献B引用了相同的参考文献,则它们之间构成耦合关系(coupling)。 它们所包含相同参考文献的个数成为耦合强度。 如果两篇文献同时引用了1篇文献,则耦合度为1;若同时引用了3篇文献,则耦合度为3。 两篇文献拥有的共同参考文献越多,则其研究内容越相似。
耦合关系的邻接矩阵可以用转置后关联矩阵的叉乘来表示。
m3 <- crossprod(t(m),t(m))
m3
## A B C
## A 2 1 1
## B 1 3 3
## C 1 3 3
文献B和C共同引用了1/2/4号文献,因此它们之间的耦合关系最强,数值为3。
g3 <- graph_from_adjacency_matrix(m3, mode = "undirected")
par(mar=c(1,1,1,1))
plot(g3)
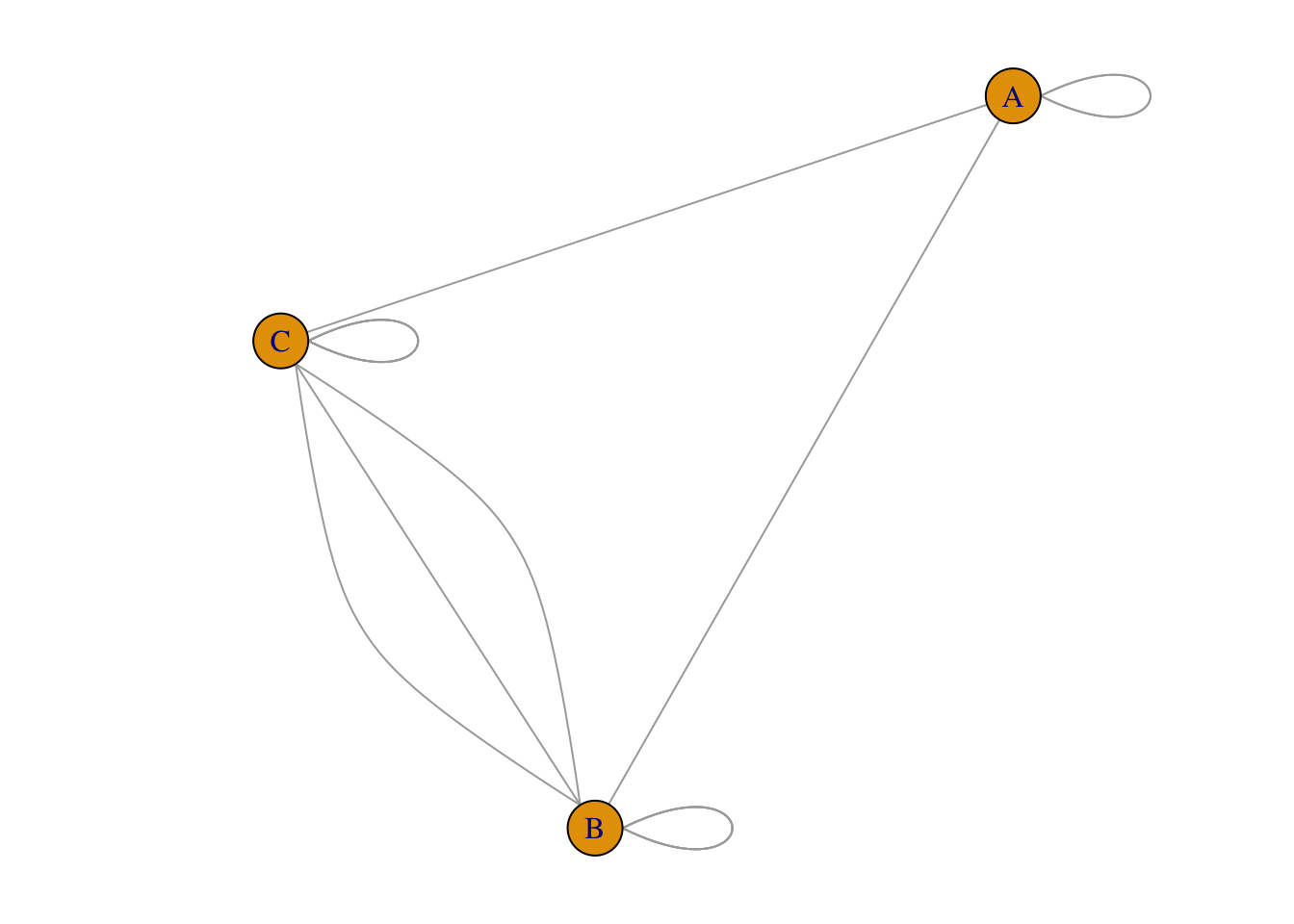
从文献耦合的概念上看,一个文献引用的参考文献越多, 那么它将有越多的机会与其它文献建立耦合关系。 为了消除这种影响,通常需要对原始数据使用 Jaccard 或 Salton 方法进行标准化处理, 来计算相对的耦合强度。
bibliometrix::normalizeSimilarity() 提供了3种方法来标准化耦合矩阵。
method <- c("association", "jaccard", "inclusion","salton", "equivalence")
m3_list <- lapply(method, function(x){
bibliometrix::normalizeSimilarity(m3,type = x)
})
names(m3_list) <- method
m3_list
## $association
## 3 x 3 sparse Matrix of class "dsCMatrix"
## A B C
## A 0.5000000 0.1666667 0.1666667
## B 0.1666667 0.3333333 0.3333333
## C 0.1666667 0.3333333 0.3333333
##
## $jaccard
## 3 x 3 sparse Matrix of class "dsCMatrix"
## A B C
## A 1.00 0.25 0.25
## B 0.25 1.00 1.00
## C 0.25 1.00 1.00
##
## $inclusion
## 3 x 3 sparse Matrix of class "dsCMatrix"
## A B C
## A 1.0 0.5 0.5
## B 0.5 1.0 1.0
## C 0.5 1.0 1.0
##
## $salton
## 3 x 3 sparse Matrix of class "dsCMatrix"
## A B C
## A 1.0000000 0.4082483 0.4082483
## B 0.4082483 1.0000000 1.0000000
## C 0.4082483 1.0000000 1.0000000
##
## $equivalence
## 3 x 3 sparse Matrix of class "dsCMatrix"
## A B C
## A 1.0000000 0.1666667 0.1666667
## B 0.1666667 1.0000000 1.0000000
## C 0.1666667 1.0000000 1.0000000
标准化的邻接矩阵最大值都不超过1,因此在创建网络的时候要使用“weighted = TRUE”模式。
这样,矩阵的强度将会转变为边的属性。
par(mfrow=c(2,3))
success <- lapply(seq_along(m3_list), function(x){
par(mar=c(1,1,1,1))
graph_from_adjacency_matrix(m3_list[[x]], mode = "undirected", weighted = TRUE) %>%
plot(main=method[[x]])
})
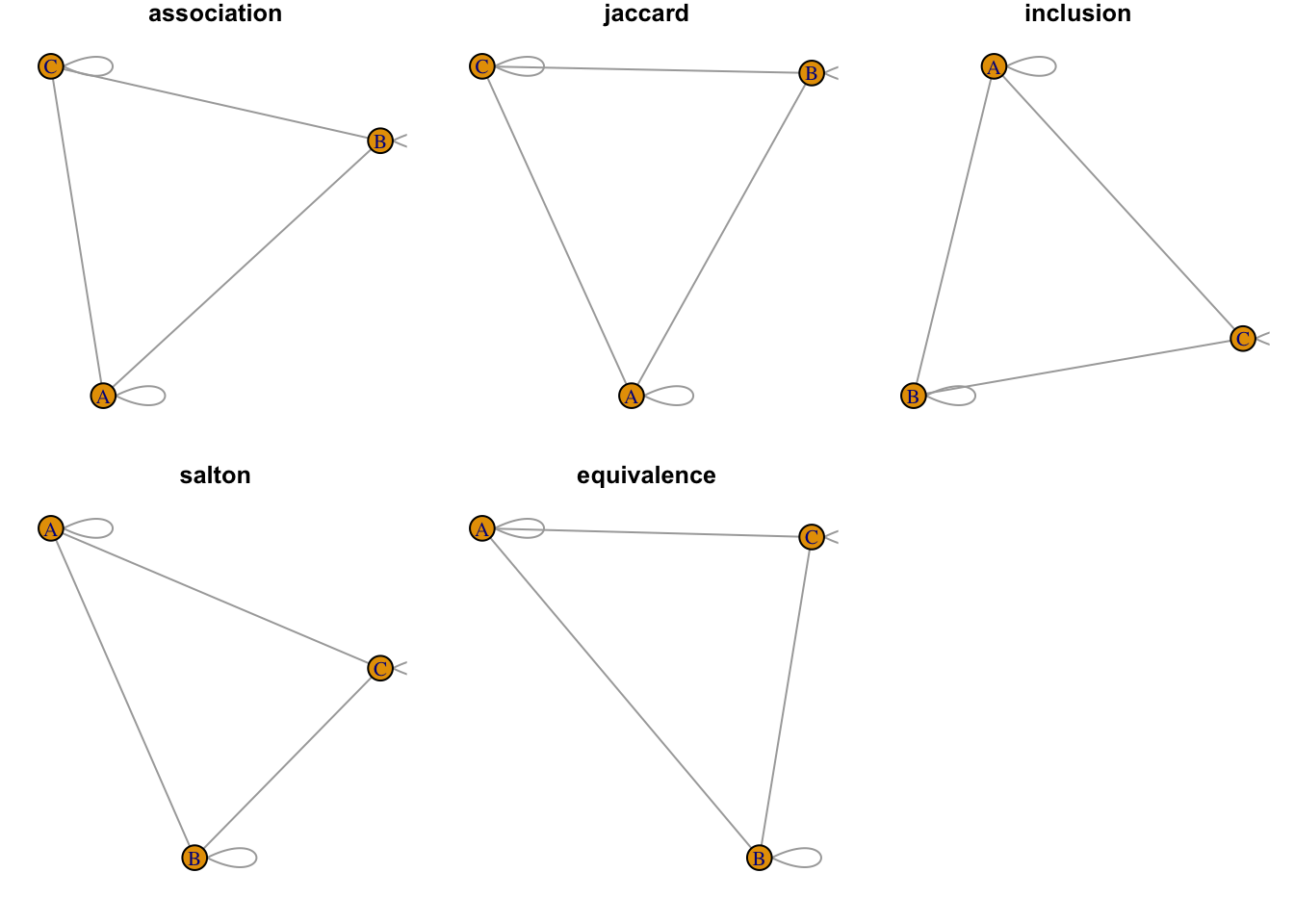
乍看上去,生成的网络是一样的,但事实上边的属性不一样。 如果我们把边的宽度映射到“weight”属性,则仍然可以发现文献B和C之间的耦合关系是最强的。
par(mfrow=c(2,3))
success <- lapply(seq_along(m3_list), function(x){
par(mar=c(1,1,1,1))
g3_weighted <- graph_from_adjacency_matrix(m3_list[[x]], mode = "undirected", weighted = TRUE)
E(g3_weighted)$width <- edge.attributes(g3_weighted)$weight*5
plot(g3_weighted, main=method[[x]])
})
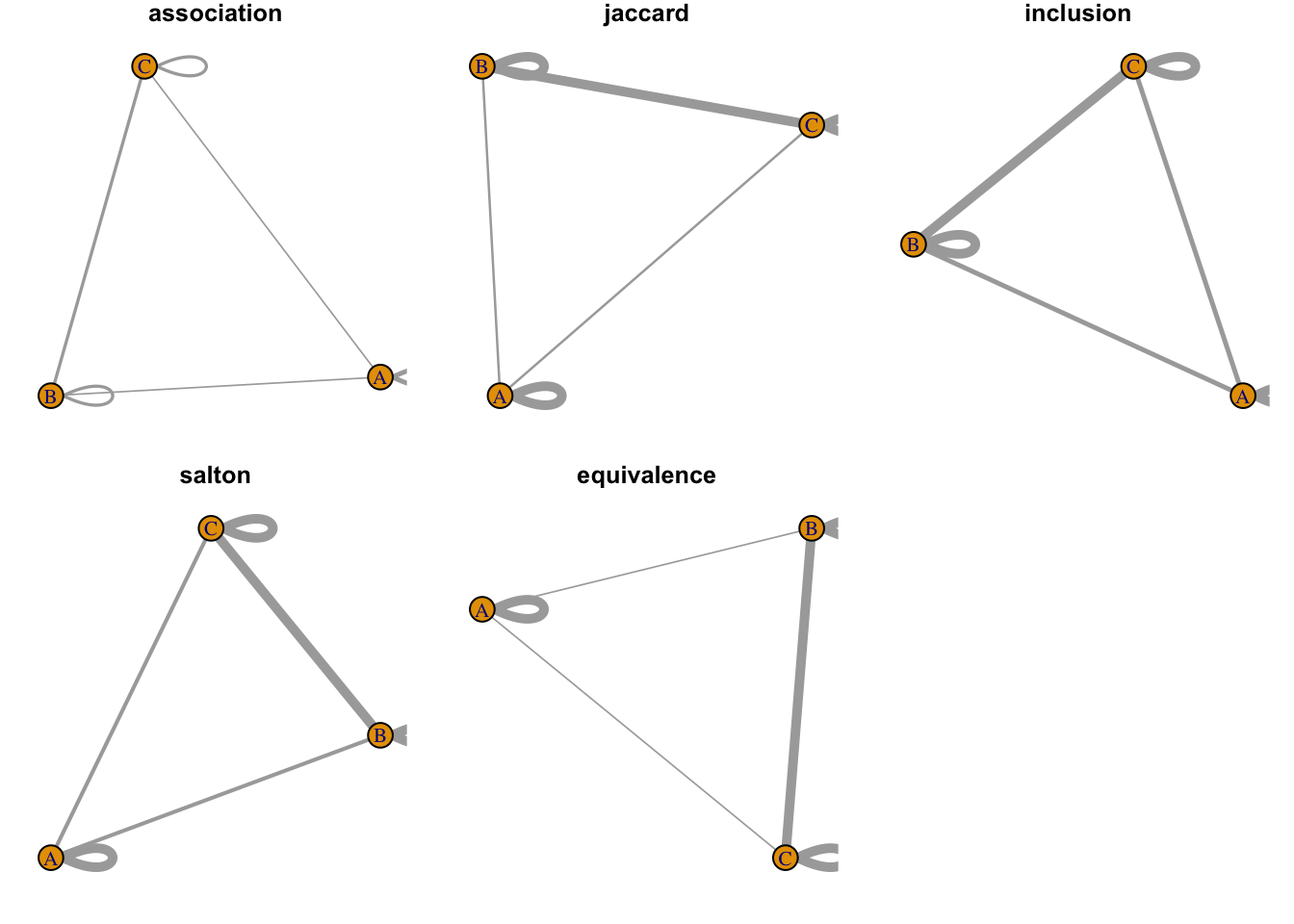
对于耦合网络来说,图中的 loop 是没有意义的。可以使用 igraph::simplify() 来去掉。
g4 <- simplify(g3, remove.multiple = FALSE, remove.loops = TRUE)
plot(g4)
