猴子吃桃问题

寒假作业上有一道题：一只猴子有很多桃子，每天都吃一半加 1 个，最后在第 4 天的时候只剩下 1 个桃子。问它原来有几个桃子？

这是一个迭代的问题，往前数第 \(n\) 天的桃子数量是 \(f(n)\)，且 \(f(n) = (f(n-1)+1) * 2\)。若 \(n = 0\)，则 \(f(0) =1\)。可以写成下面的形式。

taozi = function(n){
  if (n == 0) return(1)
  (taozi(n-1) + 1) * 2
}

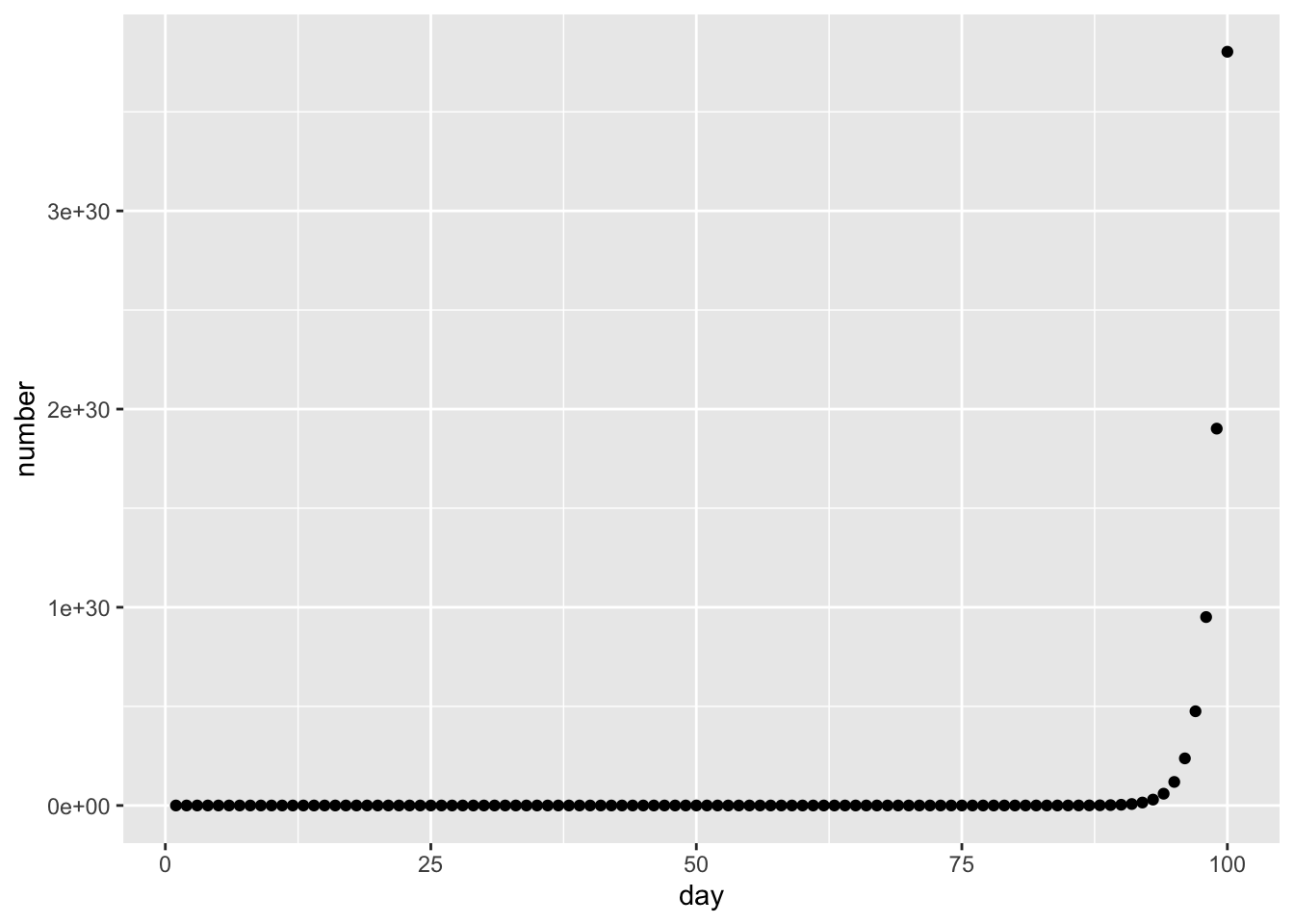
如果花了 100 天才剩下 1 个桃子，那么原有的桃子数量将会很多（3.8029518\times 10^{30} 个）。

x = 1:100
y = sapply(1:100, taozi)

library(dplyr, quietly = TRUE)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

library(ggplot2)
df = tibble(day = x, number = y)

# 桃子数量
ggplot(df, aes(day, number)) + geom_point()

# 对桃子数量进行 log 变换，得到线性关系
ggplot(df, aes(day, number)) + geom_point() + scale_y_log10()

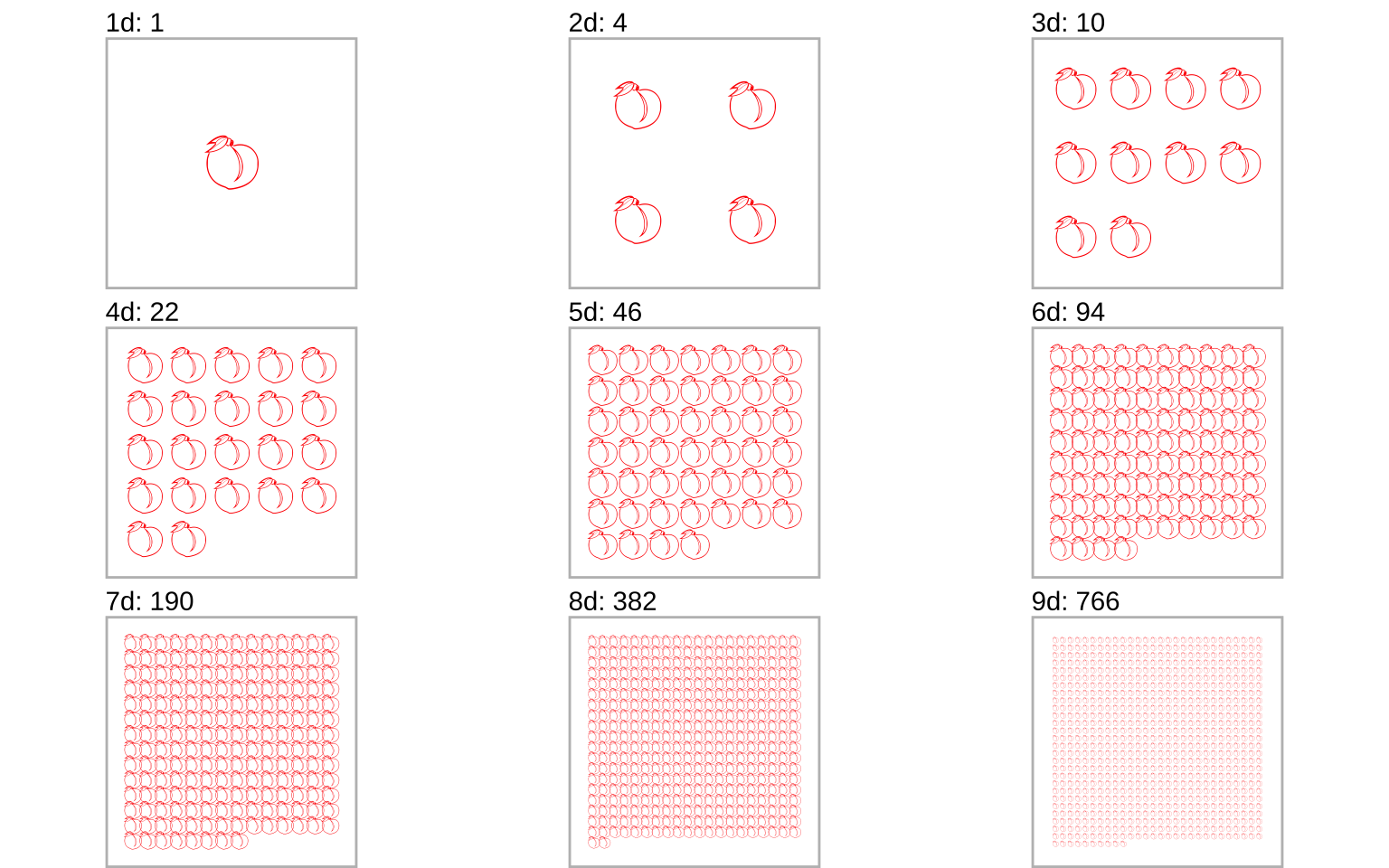
为了更加形象的展示这种变化，不妨祭出 emojifont 软件包，再施加一些魔法，可以得到 1 - 9 天情况下桃子的数量。

# 根据桃子数量生成一个正方形矩阵
grid = function(n){
  i = ceiling(sqrt(n))
  tibble(
    x = rep(1:i, length.out = i^2),
    y = rep(i:1, each =i)
  )
}

library(emojifont)
plots = lapply(1:9, function(x){
  t = taozi(x-1)
  g = grid(t)[1:t,]
  ggplot() + 
    geom_emoji("peach", x = g$x, y = g$y, size = 10 - x, color = "red1") +
    coord_equal() +
    theme_void() +
    scale_x_continuous(expand = expansion(0.1, 0.5)) +
    scale_y_continuous(expand = expansion(0.1, 0.5)) +
    labs(subtitle = paste0(x, "d: ", t)) +
    theme(panel.border = element_rect(color = "grey", linewidth = 1, fill = NA))
})

cowplot::plot_grid(plotlist = plots, align = "hv")