GSEA原理及其在微生物组数据的广义化应用

gaoch

2025-11-21

GSEA分析的统计学核心原理

GSEA（Gene Set Enrichment Analysis，基因集富集分析）是一种基于阈值的计算方法，其核心统计学目标是判断一个预先定义的基因集（Gene Set）内的基因，是否在两个生物学状态（例如肿瘤组织 vs 正常组织）的基因表达排序列表中呈现非随机的排列。不同于传统的差异表达分析（只关注差异显著的少数基因），GSEA关注的是整个基因表达谱的整体趋势，利用加权柯尔莫哥洛夫-斯米尔诺夫（Kolmogorov-Smirnov）统计量来评估整体富集程度。

基因排序与富集分数的计算

GSEA算法的第一步并非筛选基因，而是对所有检测到的基因进行全量排序，随后通过特定的“游走”算法计算富集分数。

基因列表的预排序

分析首先需要建立一个排序的基因列表（Ranked Gene List）。根据基因表达量与表型（Phenotype）的相关性计算统计量（如Signal-to-Noise Ratio, t-test statistic, Pearson correlation等）。

如果基因在实验组高表达，它会被排在列表的顶部；如果在对照组高表达，则排在列表底部；若无差异，则处于中间。这一步将生物学问题转化为了一个有序的数学序列。

游走算法与KS统计量

这是GSEA的核心算法步骤。为了计算某个特定基因集（例如“细胞周期通路”）的富集分数（Enrichment Score, ES），算法会从上到下遍历上述的排序基因列表：

当遇到属于该基因集的基因时，累积统计量增加（加分）；
当遇到不属于该基因集的基因时，累积统计量减少（减分）。

增加和减少的幅度与该基因与表型的相关性强度有关（加权）。富集分数（ES）就是这个随机游走过程中偏离零点的最大偏差值。如果基因集的成员主要集中在列表顶部，ES为正值；若集中在底部，ES为负值；若均匀分布，ES接近于零。这本质上是一种加权的Kolmogorov-Smirnov样统计量。

显著性评估与多重假设检验

计算出ES值后，必须从统计学上判断该分数是否仅仅是由随机因素造成的，以及在同时检测成百上千个基因集时如何控制假阳性。

置换检验建立零假设分布

为了获得P值，GSEA采用置换检验（Permutation Test）。通常的做法是保持基因表达数据不变，随机打乱样本的表型标签（Phenotype Permutation）。

通过上千次的随机打乱，重新计算该基因集在随机状态下的ES值，从而生成一个经验性的零假设分布（Null Distribution）。将实际观测到的ES值与这个零分布进行比较，计算出经验P值（Nominal P-value）。这种方法保留了基因之间复杂的共表达结构（Correlation structure），比简单的基因随机抽样更符合生物学实际。

归一化富集分数

由于不同的基因集包含的基因数量差异很大（有的含10个基因，有的含500个），较大的基因集往往更容易获得较大的ES绝对值。为了在不同基因集之间进行横向比较，必须消除基因集大小的影响。

通过对ES进行标准化处理，得到归一化富集分数（Normalized Enrichment Score, NES）。NES是实际ES值除以同等大小基因集在零分布中的平均ES值计算得出的。NES是比较不同通路富集程度的主要指标。

错误发现率

在一次分析中通常会测试数千个基因集，多重假设检验会导致假阳性累积。GSEA不使用传统的Bonferroni校正（过于保守），而是采用错误发现率（False Discovery Rate, FDR）进行控制。

通过计算q-value，估算在给定的NES阈值下，发现的显著基因集中可能有多少比例是假阳性。通常设定FDR < 0.25或< 0.05作为显著性的筛选标准，这比P值更具参考价值。

核心富集基因的界定

GSEA不仅给出评分，还能定位起关键作用的基因。

前导边缘分析

在得到显著富集的基因集后，研究者往往关心具体是哪些基因导致了这种富集。这部分基因被称为前导边缘子集（Leading Edge Subset）。

对于正向富集的基因集，它是从列表顶部开始，直到ES达到最大值（峰值）出现之前的所有该基因集内的基因。这些基因是该通路在实验条件下发生变化的核心驱动因素，具有最高的生物学解释价值。

基于秩次统计的广义化应用原理

GSEA本质上不依赖于生物学背景，而是一种通用的非参数统计方法。其核心逻辑是检验“某个预定义的子集成员是否倾向于聚集在一个排序列表的顶部或底部”。只要数据满足“全量排序”和“类别标签”这两个条件，就可以应用这种“富集”分析的思想。

数据映射与数学抽象

要将GSEA思想应用于非生物学数据，首先需要将通用数据映射到算法所需的两个核心输入要素上。

排序列表的构建

在生物学中，这是基因列表。在通用场景下，这可以是任何具有度量值的实体列表。你需要选择一个通过数值可以量化的指标（Metric）对所有实体进行排序。

例如，在电商分析中，实体可以是“商品”，排序指标可以是“销售增长率”或“用户评分”；在人力资源分析中，实体可以是“员工”，排序指标可以是“绩效考核分数”。关键在于这个列表必须是有序的，且包含了所有关注的观测对象，而不仅仅是头部或尾部对象。

类别的定义与集合映射

在生物学中，这是基因集（通路）。在通用场景下，这是具有共同属性的实体集合。

继续上述例子，在电商中，类别可以是“品牌”、“产地”或“品类”（如电子产品、家居用品）；在人力资源中，类别可以是“部门”、“入职年份区间”或“学历背景”。如果我们要分析“某个品牌是否显著占据了高增长商品的行列”，这个品牌下的所有商品就构成了一个“集合（Set）”。

统计检验的核心逻辑

将数据映射后，评估类别对排序影响的过程，实际上就是验证该类别在序列分布上的非随机性。

它是非参数检验的一种变体

GSEA所使用的加权Kolmogorov-Smirnov（KS）统计量，本质上是在比较两个累积分布函数。在通用数据中，零假设（Null Hypothesis）是：某个特定的类别（如品牌A）的成员，均匀且随机地散布在整个排序列表（如所有商品的销量排名）中。

如果计算出的富集分数（ES）很高，且显著性检验（P值）通过，则拒绝零假设。这意味着该类别对排序指标有显著影响——例如，品牌A的商品系统性地集中在销量榜的头部，说明品牌因素对销量有正向的“富集”作用。

评估类别对排序的整体贡献

传统的分析可能只比较不同类别的均值（如T检验），但这容易被异常值影响，且忽略了整体分布形态。利用GSEA思想，可以捕捉到更细微的趋势。

例如，某类别的均值可能并不高，但其大部分成员都密集分布在排序列表的前20%区间内，这种“协同趋势”通过均值比较难以发现，但通过基于秩次的富集分析可以敏锐地检测出来。这能回答“是否属于该类别的个体倾向于获得更高的排名”这一问题。

实际应用场景举例

为了更好地理解这种迁移应用，可以构建几个具体的非生物学场景。

商业与市场分析

假设你有一份所有门店的年度利润增长率排名列表。你想知道“位于一线城市的门店”是否表现更好。

排序列表：所有门店按增长率从高到低排序。
集合：所有标记为“一线城市”的门店。
分析结果：如果计算出显著的正向NES值，说明“一线城市”这个类别属性对高增长率有显著贡献，即该类门店在榜单头部富集。

文本挖掘与情感分析

假设你有一篇文章中所有单词的使用频率排序列表。你想知道“表达愤怒情绪的词汇”是否在该文章中过度出现。

排序列表：文章中所有单词按出现频率排序。
集合：预定义的“愤怒情绪”词典。
分析结果：如果愤怒词汇显著富集在频率列表顶部，说明该文章的主旨受到愤怒情绪类别的强烈影响。

基于样本秩次的微生物群落特征富集分析策略

在经典GSEA中，我们对“基因”排序来检测“通路”的富集；而在微生物群落结构分析的场景中，是对“样本（Sample）”进行排序，来检测“样本特征（Metadata）”的富集。这种方法在统计学上是完全成立的，通常被称为样本级富集分析（Sample-Level Enrichment Analysis, SLEA）的一种变体。

构建以样本为核心的分析框架

要实现这一分析，首先需要打破传统OTU表的行列思维，将生物学问题映射到秩次统计的数学模型中。

数据的角色转换与映射

为了适配GSEA算法，你需要对OTU表和元数据（Metadata）进行如下的角色重定义：

排序实体（原基因位置）： 这里的实体不再是OTU或物种，而是你的样本（Samples）。假设你有100个样本，这100个样本就是待排序的列表元素。

排序指标（原表达量/统计量）： 排序的依据是目标菌（Bacterium X）的相对丰度。你需要提取该菌在所有样本中的丰度值，并以此为标准对100个样本进行从高到低的排序。

富集集合（原基因集/通路）： 这里的集合不再是KEGG或GO通路，而是样本的特征分组。例如，如果你的元数据中有“分组（对照组/实验组）”、“pH值（高/低）”、“采集地点”等信息，每一个类别（如“实验组”的所有样本ID组成的列表）就是一个“特征集（Feature Set）”。

具体实施步骤

这一过程可以通过R语言或Python中的相关包来实现，不需要安装GSEA的图形化软件，因为标准软件难以直接处理这种转置的数据结构。

排序向量的生成

首先需要从OTU表中提取目标数据。锁定你关注的那一个特定菌属或OTU，提取其在所有样本中的丰度数值。

构建一个命名向量（Named Vector）。向量的数值是该菌的相对丰度，向量的名称（Name/Index）是样本的ID。务必对这个向量进行降序排列（从丰度最高到最低）。如果存在大量零值（即该菌在很多样本中未检出），建议根据实际情况决定是保留零值均作为末尾，还是仅分析检出该菌的样本序列。

特征集合的字典构建

将样本的元数据（Metadata）转换为集合列表（List of Sets）。你需要遍历元数据的每一列特征，将其转化为样本ID的集合。

对于离散型变量（如分组：Deal/Control）：直接提取属于“Deal”组的所有样本ID，组成集合A；提取属于“Control”组的所有样本ID，组成集合B。

对于连续型变量（如BMI、环境因子）： GSEA处理连续变量需要先将其离散化。你可以根据中位数或四分位数，将连续变量划分为“High_Level”和“Low_Level”两个类别的样本集合。

算法运算与统计检验

利用支持自定义背景集的GSEA工具包进行计算。推荐使用R语言中的fgsea或clusterProfiler包。

将上述准备好的“排序样本向量”作为stats输入，将“特征集合列表”作为pathways输入。设置排列次数（nperm）通常为1000或10000次。运行算法后，程序会计算每个特征集合在样本排序列表中的富集分数（ES）和显著性（P值）。

结果解读与生物学意义

这种分析方式能挖掘出比常规差异分析更丰富的群落生态学规律。

理解富集分数（NES）

正向NES（NES > 0）： 表示该特征集合（如“高pH环境样本集”）主要集中在排序列表的顶部。这意味着，具有该特征的样本倾向于拥有更高的目标菌相对丰度。

负向NES（NES < 0）： 表示该特征集合主要集中在排序列表的底部。这意味着，具有该特征的样本倾向于拥有更低的目标菌相对丰度。

识别核心驱动样本（Leading Edge）

通过Leading Edge分析，你可以找出具体是哪些样本导致了显著性。例如，发现“患病组”显著富集在“某致病菌”的高丰度端，你可以进一步查看Leading Edge中的样本ID，这些样本就是该菌爆发的核心宿主。

相比传统方法的优势

相比于直接比较两组样本中该菌丰度的均值（Wilcoxon秩和检验），这种方法的优势在于：

鲁棒性： 对异常值不敏感，关注的是整体分布趋势。
多维度： 可以同时一次性评估几十种环境因子或临床指标对该菌分布的影响，快速筛选出关键的环境驱动因子。

使用fgsea进行样本特征富集分析的R语言实例

这是一个基于R语言包 fgsea 的完整实例。为了让你能够直接运行并理解流程，我首先构建了一组模拟的OTU表和元数据，然后演示如何将“元数据列”转化为“基因集列表”，最后进行富集分析。

数据准备与环境配置

首先加载必要的包。如果没有安装，请先使用 install.packages("fgsea") 和 install.packages("tidyverse")。

模拟数据生成

这里模拟了50个样本，包含一个目标菌（Bacterium_X）和两个元数据特征（分组和来源）。

suppressPackageStartupMessages({
  library(fgsea)
  library(tidyverse)
})

# 1. 模拟数据构建
set.seed(123)
sample_ids <- paste0("Sample_", 1:50)

# 模拟元数据 (Metadata)
# 包含两个分类变量：分组(Group) 和 来源(Source)
metadata <- data.frame(
  SampleID = sample_ids,
  Group = sample(c("Control", "Treatment"), 50, replace = TRUE),
  Source = sample(c("Fecal", "Oral"), 50, replace = TRUE),
  row.names = sample_ids
)

# 模拟目标菌的相对丰度向量
# 假设 Treatment 组的丰度普遍稍高一点，以便最后能跑出结果
raw_abundance <- numeric(50)
names(raw_abundance) <- sample_ids

for(id in sample_ids) {
  base_val <- runif(1, 0, 100)
  # 如果是处理组，人为增加一点丰度，制造差异
  if(metadata[id, "Group"] == "Treatment") {
    base_val <- base_val + runif(1, 20, 50)
  }
  raw_abundance[id] <- base_val
}

# 查看一下数据结构
head(metadata)

##          SampleID     Group Source
## Sample_1 Sample_1   Control   Oral
## Sample_2 Sample_2   Control  Fecal
## Sample_3 Sample_3   Control  Fecal
## Sample_4 Sample_4 Treatment  Fecal
## Sample_5 Sample_5   Control  Fecal
## Sample_6 Sample_6 Treatment   Oral

head(raw_abundance)

##  Sample_1  Sample_2  Sample_3  Sample_4  Sample_5  Sample_6 
##  59.99890  33.28235  48.86130 129.93445  89.03502 129.70587

数据标准化

这是最关键的统计学问题。

微生物组的数据现状： 微生物相对丰度全部大于或等于0。如果你直接用原始丰度做 Stats，Running Sum 只会一直往上加，永远不会下降，这会导致统计分布偏倚，无法正确评估“低丰度”区域的富集。
GSEA的原生逻辑： 默认的 scoreType = "std" 假设排序指标（Stats）有正有负（例如基因表达的 log2FoldChange，上调为正，下调为负）。算法在计算富集分数（Running Sum）时，遇到正值累加，遇到负值扣减，从而形成“峰值”。

# 【修正点 A】：对丰度进行 Z-score 标准化
# 这样可以将非负的丰度值转换为以0为中心的正负值
# 高于均值的变为正数，低于均值的变为负数
abundance_zscore <- (raw_abundance - mean(raw_abundance)) / sd(raw_abundance)

构建排序列表与特征集合

这是分析中最关键的一步，需要将数据格式转换为 fgsea 能够识别的格式。

步骤一：构建排序向量 (Stats)

对应 GSEA 中的“基因排序列表”，这里是按目标菌丰度排序的样本列表。

# 2. 准备排序向量 (Ranked List)
# 对样本按照目标菌丰度从高到低排序
ranked_samples <- sort(abundance_zscore, decreasing = TRUE)

# 查看前几个样本（丰度最高的样本）
head(ranked_samples)

## Sample_28  Sample_4  Sample_6 Sample_27  Sample_8 Sample_35 
##  1.854213  1.820532  1.814276  1.706533  1.618897  1.511349

步骤二：构建特征集合列表 (Pathways)

对应 GSEA 中的“通路列表”，这里是将元数据特征转化为样本ID集合。

# 3. 构建特征集合 (Sets / Pathways)
# 我们需要一个 list，list 的名字是特征名，内容是属于该特征的样本ID向量

# 方法：遍历元数据感兴趣的列，使用 split 函数快速分组
metadata_cols <- c("Group", "Source") # 指定要分析的列
sample_sets <- list()

for (col in metadata_cols) {
  # 将样本ID按照该列的分类进行拆分
  # 例如：Group 列会被拆分为 "Group_Control" 和 "Group_Treatment" 两个集合
  split_list <- split(rownames(metadata), metadata[[col]])
  
  # 为了结果清晰，给集合名字加上列名前缀
  names(split_list) <- paste0(col, "_", names(split_list))
  
  # 加入总列表
  sample_sets <- c(sample_sets, split_list)
}

# 查看生成的集合结构
str(sample_sets)

## List of 4
##  $ Group_Control  : chr [1:30] "Sample_1" "Sample_2" "Sample_3" "Sample_5" ...
##  $ Group_Treatment: chr [1:20] "Sample_4" "Sample_6" "Sample_7" "Sample_8" ...
##  $ Source_Fecal   : chr [1:27] "Sample_2" "Sample_3" "Sample_4" "Sample_5" ...
##  $ Source_Oral    : chr [1:23] "Sample_1" "Sample_6" "Sample_7" "Sample_9" ...

# 输出示例：
# $ Group_Control : chr [1:26] "Sample_2" "Sample_4" ...
# $ Group_Treatment: chr [1:24] "Sample_1" "Sample_3" ...

运行富集分析与可视化

使用核心函数 fgsea 进行计算。

# 4. 运行 fgsea 分析
fgseaRes <- fgsea(
  pathways = sample_sets,   # 你的特征集合列表
  stats    = ranked_samples, # 你的排序样本向量
  minSize  = 5,              # 集合中最少样本数（太少不分析）
  maxSize  = 500            # 集合中最多样本数
)

# 5. 结果整理与展示
# 按照 NES (归一化富集分数) 排序
fgseaRes_tidy <- fgseaRes %>%
  arrange(desc(NES)) %>%
  select(pathway, pval, padj, NES, size)

print(fgseaRes_tidy)

##            pathway         pval         padj        NES  size
##             <char>        <num>        <num>      <num> <int>
## 1: Group_Treatment 1.896680e-07 3.793361e-07  2.5942035    20
## 2:     Source_Oral 6.013865e-01 8.018486e-01  0.8920200    23
## 3:    Source_Fecal 9.763113e-01 9.763113e-01  0.5533213    27
## 4:   Group_Control 8.471189e-08 3.388475e-07 -2.7103134    30

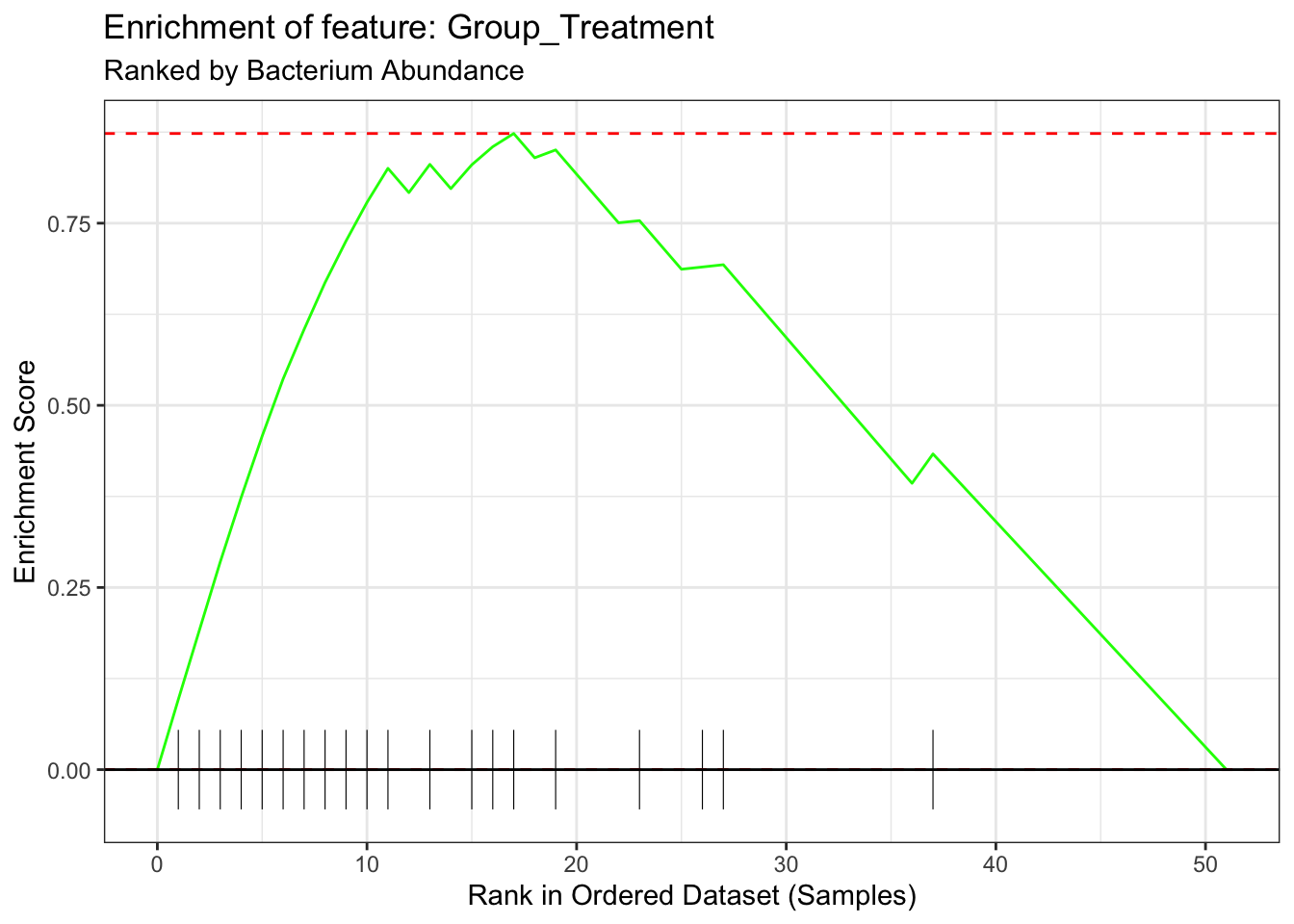
# 6. 可视化 (Enrichment Plot)
# 绘制富集程度最高的那个特征
top_pathway <- fgseaRes_tidy$pathway[1]

plotEnrichment(sample_sets[[top_pathway]], ranked_samples) + 
  labs(title = paste("Enrichment of feature:", top_pathway),
       subtitle = "Ranked by Bacterium Abundance",
       x = "Rank in Ordered Dataset (Samples)",
       y = "Enrichment Score") +
  theme_bw()

结果解读指南

运行上述代码后，你需要关注 fgseaRes_tidy 表格中的几个关键指标：

NES (Normalized Enrichment Score)

NES > 0 (正值): 表示该组样本（如 Group_Treatment）主要聚集在排序列表的左侧（顶部）。 含义： Group_Treatment 这一特征与该菌的高丰度正相关。
NES < 0 (负值): 表示该组样本主要聚集在排序列表的右侧（底部）。 含义： 该特征与该菌的低丰度相关。

padj (Adjusted P-value)

如果 padj < 0.05，说明这种聚集不是随机发生的，具有统计学显著性。

可视化图 (Barcode Plot)

X轴： 代表所有样本，从左到右该菌丰度依次降低。
黑色竖线： 代表属于该特征（如 Group_Treatment）的样本所在的位置。
绿色曲线： 富集分数的走势。如果曲线在左侧高高隆起，说明该特征的样本显著富集在高丰度区域。

GSEA前导边缘分析：识别核心驱动样本

Leading Edge Analysis（前导边缘分析）是GSEA结果解读中至关重要的一步,能够帮助我们定位哪些具体元素对富集信号贡献最大。

前导边缘子集的定义

前导边缘子集（Leading Edge Subset）被定义为：从排序列表的起始位置开始，一直到出现富集分数最大值（Peak）的那一刻为止，在此区间内出现的所有属于该特征集合的成员。

在经典的基因集富集分析中，这些成员是基因；而在本文介绍的样本级富集分析中，这些成员是样本ID。前导边缘子集被认为是该特征集合富集信号的核心贡献者。

在微生物组分析中的意义

在微生物群落分析场景中，前导边缘样本具有特殊的生物学意义：

识别关键宿主样本： 当我们发现某个样本特征（如"患病组"）在某个菌的高丰度端显著富集时，前导边缘子集包含的样本ID就是该菌丰度最极端的核心样本。这些样本可能代表了疾病最严重的个体，或是环境因子作用最强烈的生态位。

筛选代表性样本： 在后续的深度测序、代谢组学或其他高成本分析中，可以优先选择前导边缘样本进行验证，因为它们最能代表该特征与目标菌丰度之间的关联模式。

提取前导边缘样本

在使用 fgsea 包进行分析时，结果表格中已经自动包含了一个名为 leadingEdge 的列。这一列是一个列表（List）结构，存储了每个特征集合的具体核心样本ID。

# 假设 fgseaRes 是之前运行得到的结果对象
# 1. 查看结果表结构，注意 leadingEdge 列
head(fgseaRes)

##            pathway         pval         padj    log2err         ES        NES
##             <char>        <num>        <num>      <num>      <num>      <num>
## 1:   Group_Control 8.471189e-08 3.388475e-07 0.70497572 -0.8474911 -2.7103134
## 2: Group_Treatment 1.896680e-07 3.793361e-07 0.69013246  0.8730745  2.5942035
## 3:    Source_Fecal 9.763113e-01 9.763113e-01 0.03911552  0.1816169  0.5533213
## 4:     Source_Oral 6.013865e-01 8.018486e-01 0.06266182  0.2937660  0.8920200
##     size                                                    leadingEdge
##    <int>                                                         <list>
## 1:    30 Sample_9,Sample_19,Sample_39,Sample_20,Sample_18,Sample_31,...
## 2:    20   Sample_28,Sample_4,Sample_6,Sample_27,Sample_8,Sample_35,...
## 3:    27  Sample_28,Sample_4,Sample_8,Sample_22,Sample_11,Sample_10,...
## 4:    23     Sample_6,Sample_27,Sample_35,Sample_32,Sample_12,Sample_48

# 2. 提取富集最显著特征的前导边缘样本
# 先按 NES 降序排列，取第一行
top_feature_info <- fgseaRes %>%
  arrange(desc(NES)) %>%
  slice(1)

# 获取特征名称
feature_name <- top_feature_info$pathway

# 获取 Leading Edge 样本列表 (这是一个 list 元素，需要 unlist)
core_samples <- unlist(top_feature_info$leadingEdge)

# 打印结果
cat("Top Feature:", feature_name, "\n")

## Top Feature: Group_Treatment

cat("Number of Core Samples:", length(core_samples), "\n")

## Number of Core Samples: 15

cat("Core Sample IDs:\n")

## Core Sample IDs:

print(core_samples)

##  [1] "Sample_28" "Sample_4"  "Sample_6"  "Sample_27" "Sample_8"  "Sample_35"
##  [7] "Sample_32" "Sample_22" "Sample_12" "Sample_48" "Sample_11" "Sample_13"
## [13] "Sample_17" "Sample_43" "Sample_40"

# 3. 提取这些核心样本的丰度值进行进一步分析
core_sample_abundance <- abundance_zscore[core_samples]
cat("\nAbundance distribution of core samples:\n")

## 
## Abundance distribution of core samples:

summary(core_sample_abundance)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.3488  0.8236  1.2385  1.2063  1.6627  1.8542

可视化前导边缘的重叠

当发现多个样本特征显著富集时，可以使用 UpSet 图来展示它们的前导边缘样本是否存在重叠。这能回答一个重要问题：不同的样本特征是否由同一批核心样本驱动？

library(UpSetR)

# 1. 筛选显著富集的特征（例如 padj < 0.05）
sig_features <- fgseaRes %>%
  filter(padj < 0.05) %>%
  arrange(desc(abs(NES)))

# 如果显著特征太多，只取前5个
if(nrow(sig_features) > 5) {
  sig_features <- sig_features %>% head(5)
}

# 2. 构建 UpSetR 需要的列表数据
# 列表名为特征名，列表内容为该特征的 leadingEdge 样本
list_for_upset <- setNames(sig_features$leadingEdge, sig_features$pathway)

# 3. 绘制 UpSet 图
# 这张图能清晰展示哪些样本是多个特征共有的（关键驱动样本）
upset(fromList(list_for_upset), 
      order.by = "freq",
      main.bar.color = "steelblue",
      sets.bar.color = "darkgreen")

## Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
## ℹ Please use tidy evaluation idioms with `aes()`.
## ℹ See also `vignette("ggplot2-in-packages")` for more information.
## ℹ The deprecated feature was likely used in the UpSetR package.
##   Please report the issue to the authors.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## ℹ The deprecated feature was likely used in the UpSetR package.
##   Please report the issue to the authors.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

## `geom_line()`: Each group consists of only one observation.
## ℹ Do you need to adjust the group aesthetic?

## Warning: The `size` argument of `element_line()` is deprecated as of ggplot2 3.4.0.
## ℹ Please use the `linewidth` argument instead.
## ℹ The deprecated feature was likely used in the UpSetR package.
##   Please report the issue to the authors.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

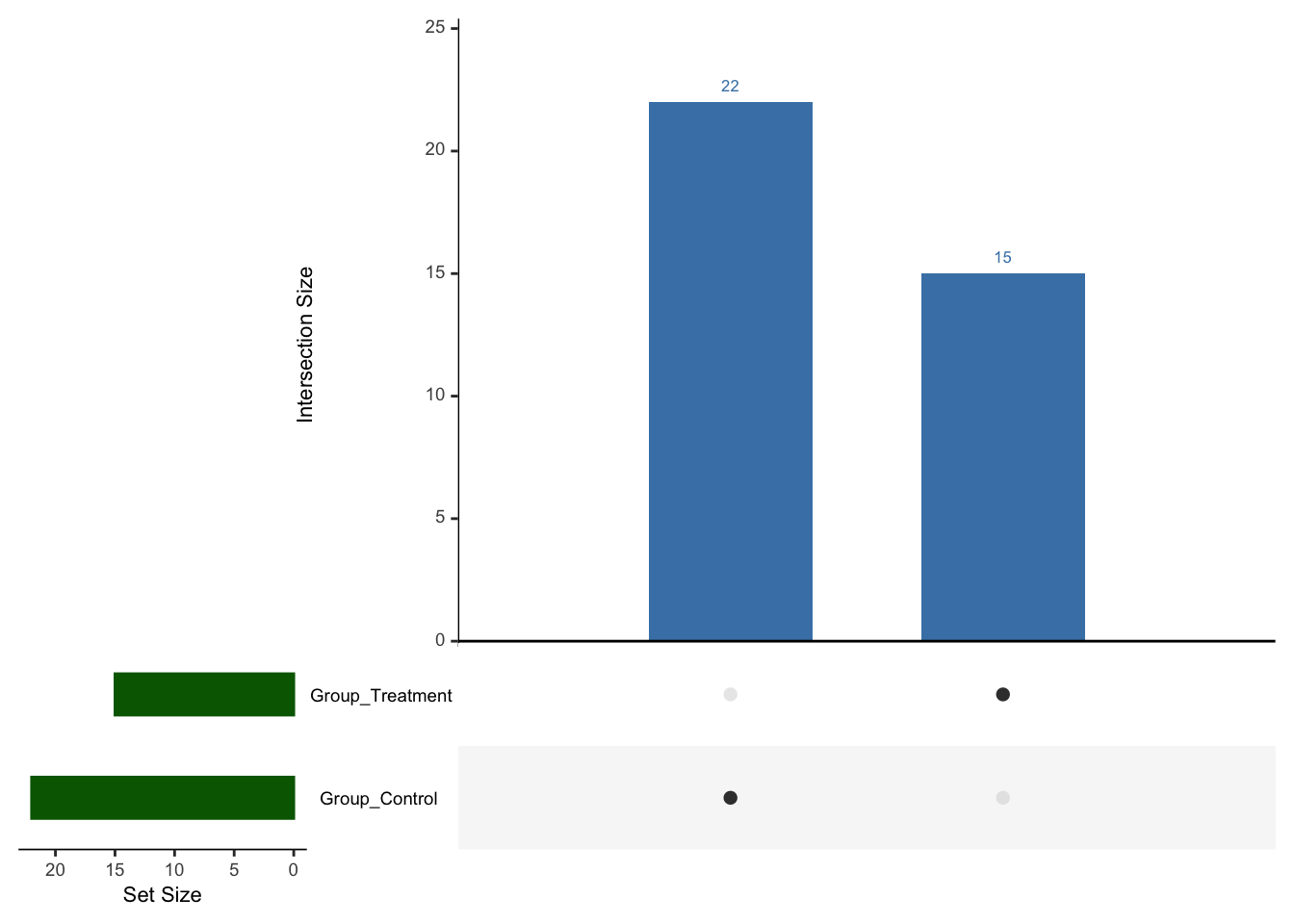
结果解读

交集部分（Intersection）： 如果多个特征的前导边缘样本存在大量重叠，说明这些样本同时具备多种极端特征。例如，某些样本可能既属于"高pH环境"又属于"患病组"的前导边缘，暗示这些特征可能协同影响目标菌的丰度分布。

特有部分： 仅属于某一个特征的前导边缘样本，则代表了该特征的独特影响。这些样本可以帮助我们区分不同环境因子或临床指标的独立效应。

生物学应用： 通过前导边缘分析识别出的核心样本，可以作为后续机制研究的重点对象，例如进行宏基因组测序、培养组学或代谢物分析，以揭示该菌与宿主/环境互作的分子机制。