样本水平富集分析

gaoch

2025-11-26

Categories: 信息技术 Tags: R 统计学

简介

样本水平富集分析 (Sample-Level Enrichment Analysis, SLEA) 是一种用于分析转录组数据集中每个样本内基因模块（或称基因集，如通路）转录状态的方法。 

主要特点和工作原理

  • 逐样本分析： 与传统的基因集富集分析 (GSEA) 不同，传统的 GSEA 通常是比较两组样本（例如，疾病组与正常组）之间基因集的富集情况，而 SLEA 是对数据集中的每个独立样本计算其特定基因集（例如，某个癌症通路）的富集得分。

  • 富集得分 (Enrichment Score)： SLEA 通过比较基因模块中基因的表达均值（或中位数）与同一样本中随机抽取的同等大小的基因集表达均值的分布，计算出一个 z-score 富集得分。这个得分反映了该基因模块在该样本中的活跃状态（上调或下调）。

  • 无需预先分组： 进行 SLEA 时，不需要预先知道样本的表型信息或临床分组，它可以直接从基因表达数据和基因集列表开始分析。

  • 可视化： 结果通常以交互式热图的形式呈现，其中行代表不同的基因模块，列代表各个样本，每个单元格显示该模块在该样本中的富集得分。这种可视化方式有助于直观地解释和识别富集模式。 

应用场景

SLEA 在生物医学研究中具有广泛的应用，包括：

  • 识别肿瘤亚型： 根据不同基因模块的富集模式对肿瘤样本进行聚类，从而发现新的分子亚型。

  • 关联分子特征与临床特征： 将富集得分与患者的临床数据（例如，生存时间、治疗反应、临床分期）相关联，以发现与特定通路活跃度相关的预后标志物。

  • 研究模块之间的关系： 探索不同信号通路或基因集在样本水平上的协同作用或拮抗关系。 

简而言之，SLEA 是一种强大的工具，能够深入挖掘单个样本的生物学特性，有助于理解疾病的异质性并发现潜在的治疗靶点。

在微生物研究领域，样本水平富集分析 (SLEA) 的应用与在人类转录组研究中的应用有相似之处，但主要集中在通过分析微生物基因表达或微生物群落的功能潜力来理解复杂的生物学过程。

在微生物研究中的应用

  1. 分析特定微生物的功能状态

    • 理解细菌适应性： 微生物基因表达的调控对于细菌在不断变化的环境条件（如肠道内的营养物质变化、宿主免疫反应）中生存和适应至关重要。SLEA 可以用于分析特定微生物在不同条件下哪些功能通路（例如，铁螯合、鞭毛合成、抗生素抗性）被激活或抑制。

    • 宿主-病原体相互作用： 在研究宿主细胞与病原体（如幽门螺杆菌 H. pylori 或结核分枝杆菌 M. tuberculosis）的相互作用时，SLEA 可用于鉴定细菌在细胞内感染期间快速适应的基因表达特征，例如与宿主粘附或营养获取相关的基因集。

  2. 整合宏基因组/宏转录组数据：

    • 在分析复杂的微生物群落（如肠道微生物组）时，研究人员通常会生成宏基因组（DNA序列）或宏转录组（RNA序列）数据。这些数据包含了群落中所有成员的基因信息。

    • 通过将这些宏组学数据映射到已知的微生物基因集文库（例如，KEGG 通路、功能基因簇），SLEA 可以评估每个样本中特定代谢或功能通路的整体活跃水平，而不仅仅是关注单个物种的丰度。

  3. 识别与疾病或环境因素相关的微生物功能模式：

    • 研究人员可以利用 SLEA 识别与特定临床特征（如炎症性肠病 IBD、肥胖、抗生素治疗反应）相关的微生物功能特征。例如，通过微生物集富集分析 (Microbe-set Enrichment Analysis, MSEA) 可以根据文献记录的微生物与哺乳动物基因的关联，将微生物分组，并找出与宿主表型相关的富集模式。

    • 在环境微生物学研究中，SLEA 可用于评估不同环境条件下（如盐度变化、污染物存在）微生物群落的功能潜力，例如氮循环、硫代谢等通路的活跃度。

  4. 结合单细胞技术：

    • 新兴的微生物单细胞测序技术可以提供更高分辨率的个体细胞功能信息。将这些技术与 SLEA 相结合，有助于确定在复杂的群落中哪些特定的细菌细胞正在利用宿主衍生的化合物或表现出特定的基因表达变化。

SLEA 在微生物研究中的应用核心在于将高通量测序数据转化为可解释的、样本特异性的功能洞见，帮助研究人员从“有哪些微生物”深入到“这些微生物在做什么”以及“它们的功能活性如何影响宿主或环境”。

R 语言示例

下面是一个用 R 语言 实现 SLEA（样本水平富集分析）的示例。

我们将使用一个流行的方法，即 ssGSEA（单样本 GSEA），这是 SLEA 的一个具体实现，通过 GSVA (Gene Set Variation Analysis) R 包来实现。

先决条件：安装必要的 R 包

你需要安装 GSVA 包以及一个用于处理示例数据的包（如 limma 或 GSEABase）。

if (!requireNamespace("BiocManager", quietly = TRUE))
    install.packages("BiocManager")

BiocManager::install("GSVA")
BiocManager::install("GSEABase")

R 语言实现示例

这个示例分为三个步骤：

  1. 准备数据： 获取一个基因表达矩阵和一些基因集（通路）。

  2. 运行 GSVA： 使用 gsva() 函数计算每个样本的富集得分。

  3. 可视化结果： 使用热图展示富集得分。

# 1. 加载必要的库
library(GSVA)
library(GSEABase)

## Loading required package: BiocGenerics

## Loading required package: generics

## 
## Attaching package: 'generics'

## The following objects are masked from 'package:base':
## 
##     as.difftime, as.factor, as.ordered, intersect, is.element, setdiff,
##     setequal, union

## 
## Attaching package: 'BiocGenerics'

## The following objects are masked from 'package:stats':
## 
##     IQR, mad, sd, var, xtabs

## The following objects are masked from 'package:base':
## 
##     anyDuplicated, aperm, append, as.data.frame, basename, cbind,
##     colnames, dirname, do.call, duplicated, eval, evalq, Filter, Find,
##     get, grep, grepl, is.unsorted, lapply, Map, mapply, match, mget,
##     order, paste, pmax, pmax.int, pmin, pmin.int, Position, rank,
##     rbind, Reduce, rownames, sapply, saveRDS, table, tapply, unique,
##     unsplit, which.max, which.min

## Loading required package: Biobase

## Welcome to Bioconductor
## 
##     Vignettes contain introductory material; view with
##     'browseVignettes()'. To cite Bioconductor, see
##     'citation("Biobase")', and for packages 'citation("pkgname")'.

## Loading required package: annotate

## Loading required package: AnnotationDbi

## Loading required package: stats4

## Loading required package: IRanges

## Loading required package: S4Vectors

## 
## Attaching package: 'S4Vectors'

## The following object is masked from 'package:utils':
## 
##     findMatches

## The following objects are masked from 'package:base':
## 
##     expand.grid, I, unname

## Loading required package: XML

## Loading required package: graph

## 
## Attaching package: 'graph'

## The following object is masked from 'package:XML':
## 
##     addNode

library(pheatmap) # 用于绘制热图

# --- 2. 准备数据 ---

# A. 准备一个示例的基因表达矩阵 (Exprs Matrix)
# 实际工作中，这是你自己的 RNA-seq 或芯片数据
# 行是基因，列是样本
# 为了演示，我们创建一个包含1000个基因和10个样本的随机数据
set.seed(123)
nr_genes <- 1000
nr_samples <- 10
expr_data <- matrix(rnorm(nr_genes * nr_samples), nrow = nr_genes)
rownames(expr_data) <- paste0("gene_", 1:nr_genes)
colnames(expr_data) <- paste0("sample_", 1:nr_samples)

# 对数据进行标准化（ssGSEA通常推荐使用非标准化数据，但我们这里简单起见使用Z-score模拟）
# 实际应用中，确保你的数据是适当的 count 或 logCPM/VST 格式
# expr_data <- apply(expr_data, 2, function(x) (x - mean(x)) / sd(x)) # 可以选择z-score标准化

# B. 准备一个基因集列表 (Gene Sets)
# 这通常是你从 MSigDB 或 KEGG 数据库下载的 GMT 文件
# 我们手动创建几个小的基因集用于演示
gene_sets <- list(
  "Pathway_A" = paste0("gene_", sample(1:nr_genes, 30)), # 包含30个基因
  "Pathway_B" = paste0("gene_", sample(1:nr_genes, 25)), # 包含25个基因
  "Pathway_C" = paste0("gene_", sample(1:nr_genes, 50))  # 包含50个基因
)

# 将列表转换为 GSEABase 要求的 GeneSetCollection 格式
gene_sets_collection <- GeneSetCollection(lapply(names(gene_sets), function(name) {
  GeneSet(gene_sets[[name]], setName = name)
}))


# --- 3. 运行 SLEA (使用 GSVA 的 ssGSEA 方法) ---

# 使用 gsva() 函数进行计算
# method="ssGSEA" 指定使用单样本富集分析方法 (即 SLEA 的一种实现)
ssparam = ssgseaParam(
  exprData = expr_data,
  geneSets = gene_sets_collection
)
slea_scores <- gsva(ssparam)

## ℹ GSVA version 2.4.1

## ℹ Searching for genes/features with constant values

## ℹ Calculating  ssGSEA scores for 3 gene sets

## ℹ Calculating ranks

## ℹ Calculating rank weights

## ℹ Normalizing ssGSEA scores

## ✔ Calculations finished

# slea_scores 是一个新的矩阵，行是基因集，列是样本，值为富集得分

print("SLEA 富集得分矩阵的前几行和列:")

## [1] "SLEA 富集得分矩阵的前几行和列:"

print(round(slea_scores[, 1:4], 3))

##           sample_1 sample_2 sample_3 sample_4
## Pathway_A    0.487    0.529    0.063    0.032
## Pathway_B    0.356    0.563    0.496    1.028
## Pathway_C    0.274    0.294    0.652    0.605

# --- 4. 可视化结果 (交互式热图) ---

# 将富集得分矩阵可视化为热图，这是 SLEA 结果最常见的展示方式
pheatmap(
  slea_scores,
  cluster_rows = TRUE,    # 对通路进行聚类
  cluster_cols = TRUE,    # 对样本进行聚类（有助于发现亚型）
  show_colnames = TRUE,
  show_rownames = TRUE,
  main = "SLEA/ssGSEA Enrichment Scrore Heatmap"
)

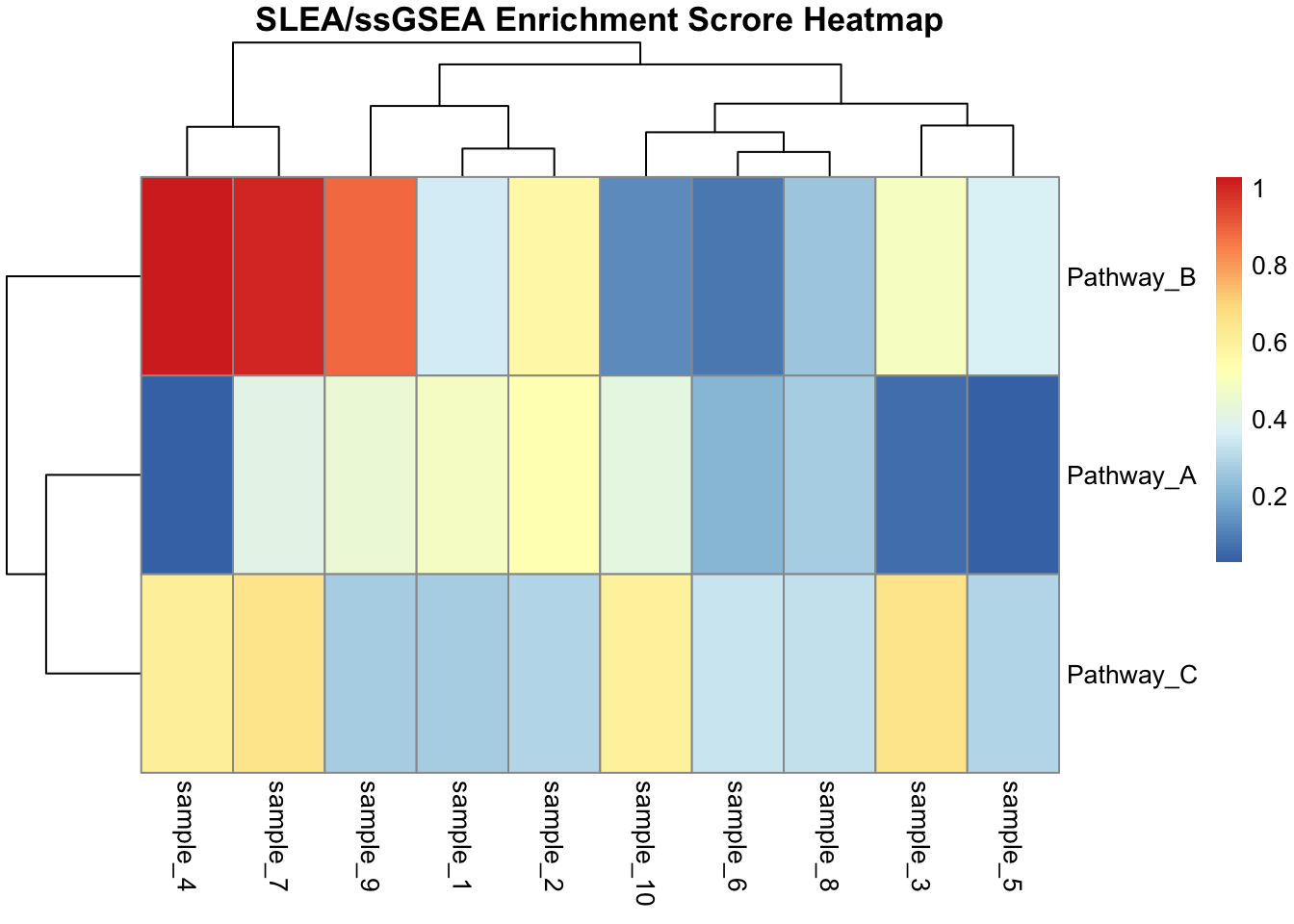
结果解释

运行上述代码后，你会得到一个名为 slea_scores 的矩阵，其中包含了每个基因集在每个样本中的富集得分（通常在 -1 到 1 之间）。

  • 正值： 表示该基因集中的基因在该样本中整体倾向于高表达（通路活跃）。

  • 负值： 表示该基因集中的基因在该样本中整体倾向于低表达（通路抑制）。

同时，R 会弹出一个热图窗口，直观地展示哪些通路在哪些样本中活跃，并且通过聚类，你可以清晰地看到样本是否自然形成了不同的亚群（正如你描述的应用场景：识别肿瘤亚型）。

关于 GSVA 软件包

GSVA 是一个功能强大的 R 语言软件包，实现了基因集变异分析 (Gene Set Variation Analysis) 方法。它是进行样本水平富集分析 (SLEA) 的核心工具，广泛应用于转录组学数据的分析中。

核心功能与特点

GSVA 软件包的主要目标是将传统的“基因中心”分析转化为“通路（基因集）中心”分析。

  • 单样本分析： 与需要比较两组样本的传统 GSEA 不同，GSVA 能够估计每个单独样本中预定义基因集（如信号通路、功能模块、免疫特征）的富集得分或活跃度。

  • 数据转换： 它将输入的“基因 × 样本”表达矩阵转换为“基因集 × 样本”的富集得分矩阵。

  • 无监督与非参数： GSVA 是一种非参数、无监督的方法，意味着它不需要预先知道样本的分组信息（如疾病 vs. 正常），使得分析更加灵活，尤其适用于高度异质性的数据集。

  • 支持多种方法： GSVA 软件包不仅实现了其同名方法 GSVA，还集成了其他三种流行的单样本富集分析方法：ssGSEA、z-score 和 PLAGE。

  • 适用性广： 它可以处理来自微阵列 (microarray) 和 RNA-seq 的基因表达数据，也可应用于其他分子谱数据，如miRNA表达、拷贝数变异 (CNV) 等。

主要应用场景

通过 GSVA 生成的富集得分矩阵，用户可以进行一系列下游分析，包括：

  • 样本聚类： 根据通路活跃度对样本进行聚类，有助于发现新的疾病亚型（如肿瘤亚型）。

  • 差异通路分析： 比较不同临床组别（如治疗前后）之间的通路活跃度差异。

  • 生存分析： 将通路富集得分与患者生存期关联，识别预后相关的通路。

  • 相关性分析： 研究不同通路之间的协同作用或拮抗关系。

四种算法

这四种算法（GSVA、ssGSEA、PLAGE、Z-score）都旨在实现样本水平富集分析（SLEA），即为每个样本计算通路活跃度得分，但它们在数学原理、标准化方法和具体实现细节上存在显著差异。

以下是它们的主要区别：

特性 GSVA (Hänzelmann et al., 2013) ssGSEA (Barbie et al., 2009) PLAGE (Tomfohr et al., 2005) Z-score (Lee et al., 2008)
方法类型 基于核密度估计 (KDE) 基于等级排序 (Rank-based) 基于奇异值分解 (SVD) 基于标准分数 (Z-score)
内部标准化 无 有 有（行/基因维度） 有（行/基因维度）
跨样本可比性 得分相对分布可比 标准化后可比 得分独立，可比 得分独立，可比
速度 较快 较慢 较快 较快

详细区别解释

1. GSVA (Gene Set Variation Analysis)

  • 原理： GSVA 使用非参数核密度估计 (KDE) 方法。它将基因表达值转换为一个排序统计量，然后根据基因集内部和外部的累积概率分布之间的差异来计算富集得分。

  • 特点： 它不需要对数据进行跨样本的标准化。GSVA 算法特别适用于处理微阵列和 RNA-seq 数据，其得分的分布通常可以提供较好的跨样本比较。它是 GSVA 软件包的默认方法。

2. ssGSEA (single sample GSEA)

  • 原理： ssGSEA 源自传统的 GSEA 方法，但将其应用于单个样本。它计算样本内所有基因的表达值排名，然后评估目标基因集中的基因是倾向于排在前面还是后面，通过累积和统计量来计算得分。

  • 特点： ssGSEA 的计算相对较慢，因为它需要对每个样本单独排序。它通常会进行额外的标准化步骤（例如将得分范围缩放到 -1 到 1 之间），以确保跨样本的可比性。

3. PLAGE (Pathway Level Analysis of Gene Expression)

  • 原理： PLAGE 基于奇异值分解 (SVD)。它将基因集看作一个“特征向量”，计算每个样本在这个特征向量上的投影分数。可以理解为寻找基因集的主要表达模式。

  • 特点： PLAGE 要求输入数据在**行维度（基因维度）**进行标准化（例如 z-score 标准化）。它的计算速度非常快，结果稳定，对样本数量不太敏感。

4. Z-score (Combined Z-score)

  • 原理： 这是最简单直观的方法。它要求输入数据在**行维度（基因维度）**进行 z-score 标准化。然后，对于一个特定的基因集，它计算该样本中所有属于该基因集的基因的 z-score 均值。

  • 特点： 计算速度快。由于基于平均值，它对离群值（Outliers）比较敏感。与 PLAGE 类似，它依赖于预先对所有基因表达值进行跨样本标准化。

总结与选择建议

  • 如果你希望使用一个默认、稳健且不需要复杂数据预处理的方法，GSVA 或 ssGSEA 是很好的选择。

  • 如果你追求极快的速度并且可以接受对基因进行预标准化，PLAGE 和 Z-score 是更快的替代方案。

在微生物研究或人类转录组研究中，这些算法的选择通常取决于研究人员的偏好和对数据特征的理解，它们通常都能提供一致的生物学见解。

算法的区别

要比较四种 SLEA 算法（GSVA、ssGSEA、PLAGE、Z-score）的结果差异，最好的方法是在同一份表达谱数据和同一组基因集上运行它们，然后比较它们生成的富集得分矩阵的相关性，并通过可视化手段直观展示。

library(corrplot)

## corrplot 0.95 loaded

# --- 3. 运行四种 GSVA 算法 ---

# A. GSVA 方法
# 使用 gsvaParam 构造函数定义参数对象
gsva_param <- gsvaParam(expr_data, gene_sets_collection)
scores_gsva <- gsva(gsva_param, verbose = FALSE)

# B. ssGSEA 方法
# 使用 ssgseaParam 构造函数定义参数对象
ssgsea_param <- ssgseaParam(expr_data, gene_sets_collection) 
# 默认 ssgsea.norm = TRUE，将分数标准化到 -1 到 1 之间
scores_ssgsea <- gsva(ssgsea_param, verbose = FALSE)

# C. PLAGE 方法
# 使用 plageParam 构造函数定义参数对象
plage_param <- plageParam(expr_data, gene_sets_collection)
scores_plage <- gsva(plage_param, verbose = FALSE)

# D. Z-score 方法
# 使用 zscoreParam 构造函数定义参数对象
zscore_param <- zscoreParam(expr_data, gene_sets_collection)
scores_zscore <- gsva(zscore_param, verbose = FALSE)


# --- 4. 结果比较与可视化 ---

# 将所有结果合并到一个数据框（或矩阵）中，以便于比较相关性
# 注意：不同方法的得分尺度不同，直接比较数值意义不大，主要看相对排序或相关性。
# 我们重点关注每种方法在所有样本中对特定通路的得分模式。

# 提取 Pathway_A 的得分，并合并到一个矩阵中
comparison_matrix <- rbind(
  "GSVA" = scores_gsva["Pathway_A", ],
  "ssGSEA" = scores_ssgsea["Pathway_A", ],
  "PLAGE" = scores_plage["Pathway_A", ],
  "Z-score" = scores_zscore["Pathway_A", ]
)
colnames(comparison_matrix) <- colnames(expr_data)

print("Pathway_A 在四种方法下的得分矩阵:")

## [1] "Pathway_A 在四种方法下的得分矩阵:"

print(round(comparison_matrix, 3))

##         sample_1 sample_2 sample_3 sample_4 sample_5 sample_6 sample_7 sample_8
## GSVA       0.043    0.205   -0.163   -0.246   -0.234   -0.072    0.025   -0.029
## ssGSEA     0.487    0.529    0.063    0.032    0.028    0.217    0.404    0.271
## PLAGE     -0.499   -0.213    0.309    0.092   -0.293   -0.248    0.463    0.259
## Z-score    0.337    1.185   -0.799   -1.213   -1.200   -0.062    0.047   -0.042
##         sample_9 sample_10
## GSVA       0.242     0.236
## ssGSEA     0.448     0.416
## PLAGE      0.352    -0.222
## Z-score    1.105     0.642

# 可视化比较：使用热图展示不同方法在不同样本间的得分差异
pheatmap(
  comparison_matrix,
  cluster_rows = FALSE, # 不对方法聚类
  cluster_cols = TRUE,  # 对样本聚类
  main = "Differences of four GSVA when applied to Pathway_A",
  scale = "row" # 按行（方法）进行标准化，使颜色具有可比性
)

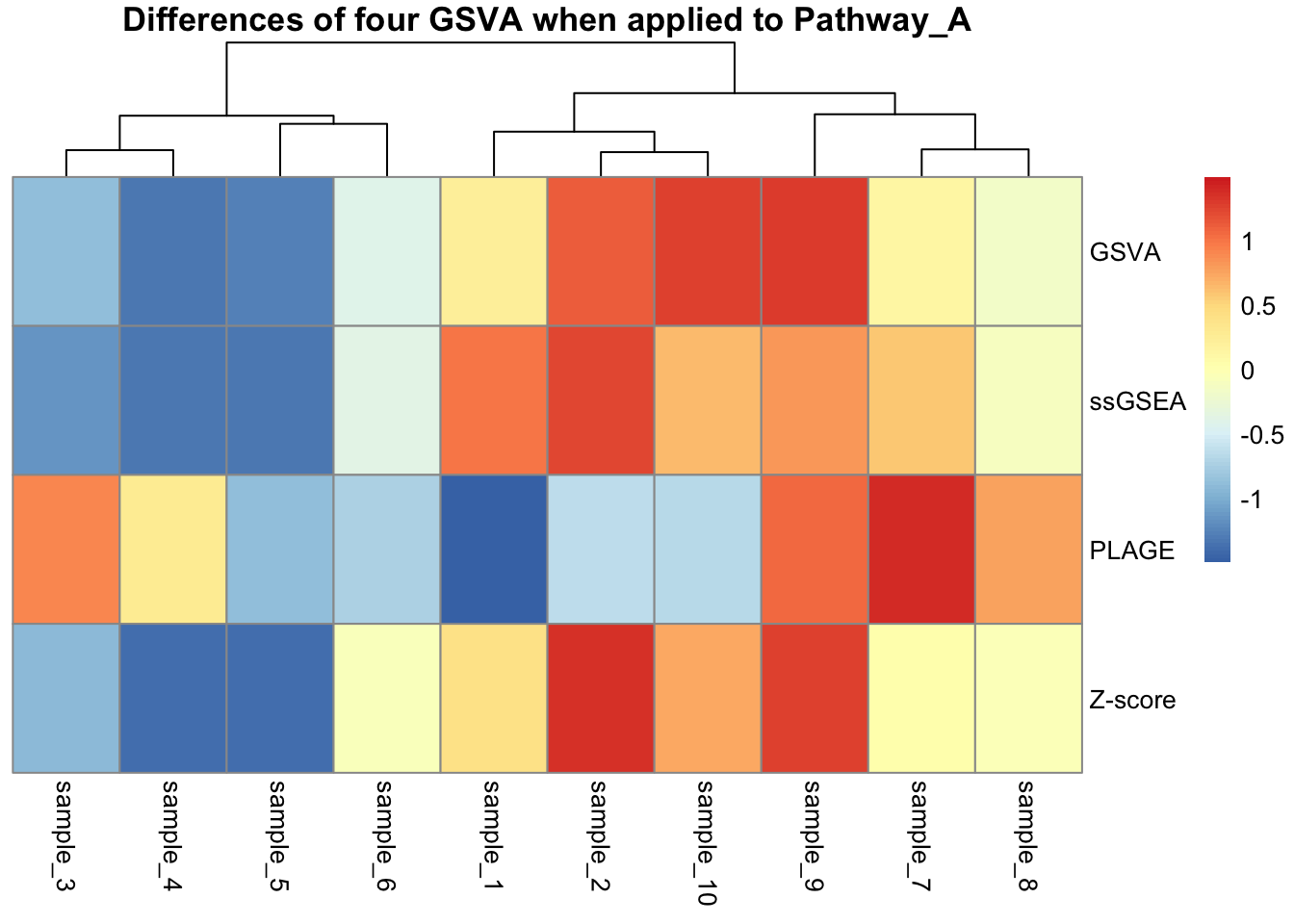
# 可视化相关性：计算不同方法之间的 Spearman 相关系数
# Spearman 相关性更适合非正态分布的富集得分
correlation_matrix <- cor(t(comparison_matrix), method = "spearman")

print("四种方法之间的 Spearman 相关性矩阵:")

## [1] "四种方法之间的 Spearman 相关性矩阵:"

print(round(correlation_matrix, 3))

##          GSVA ssGSEA PLAGE Z-score
## GSVA    1.000  0.891 0.139   0.964
## ssGSEA  0.891  1.000 0.018   0.952
## PLAGE   0.139  0.018 1.000   0.103
## Z-score 0.964  0.952 0.103   1.000

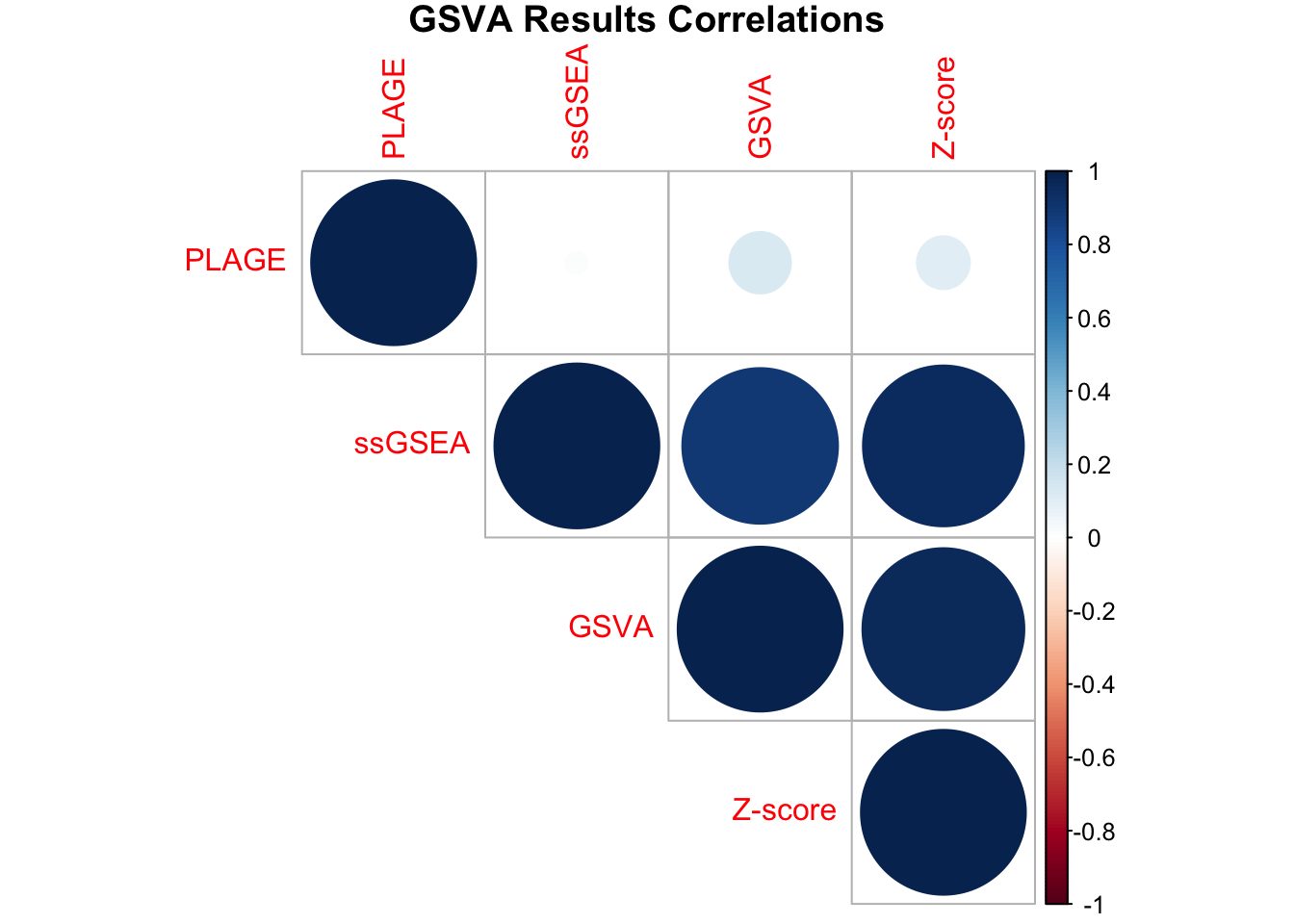
# 使用 corrplot 进行可视化
corrplot(correlation_matrix, method = "circle", type = "upper", order = "hclust",
         title = "GSVA Results Correlations", mar=c(0,0,1,0))

作者简介

Chun-Hui Gao is a Research Associate at Huazhong Agricultural University.

重复使用

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. The source code is licensed under MIT. The full source is available at https://github.com/yihui/hugo-prose.

欢迎修订

如果您发现本文里含有任何错误（包括错别字和标点符号），欢迎在本站的 GitHub 项目里提交修订意见。

引用本文

如果您使用了本文的内容，请按照以下方式引用：

gaoch (2025). 样本水平富集分析. BIO-SPRING. /post/2025/11/26/sample-level-enrichment-analysis/

BibTeX citation

@misc{
  title = "样本水平富集分析",
  author = "gaoch",
  year = "2025",
  journal = "BIO-SPRING",
  note = "/post/2025/11/26/sample-level-enrichment-analysis/"
}